Penrose On Whether A Platonic Objectivity Can Exist Independent of Human Minds.

I have been rereading certain sections of The Road To Reality by the famous mathematical physicist Roger Penrose as he touches on many things near and dear to my heart.  One of these things is whether there is a real existence of objective truth independent of human minds. Penrose seems to argue such objective frameworks probably do exist and uses math as an example. He also admits by analogous reasoning one may argue an objective morality or aesthetics beyond the minds of men may also exist but in this book he is only concerned with the math. Now to quote Penrose:

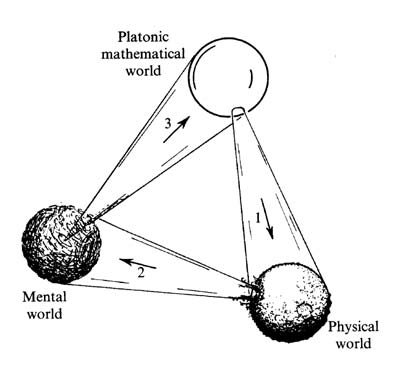
Platonic existence, as I see it, refers to the existence of an objective external standard that is not dependent upon our individual opinions nor upon our particular culture. Such 'existence' could also refer to things other than mathematics, such as to morality or aesthetics, but I am here concerned just with mathematical objectivity, which seems to be a much clearer issue...

Plato himself would have insisted that there are two other fundamental absolute ideals, namely that of the Beautiful and that of the Good. I am not at all adverse to admitting the existence of such ideals, and to allowing the Platonic world to be extended so as to contain absolutes of this nature.

And now for his reasoning about math.  Though he can't prove it, he seems to believe that belief in a real objective mathematics independent of man is necessary in order to trust it and make progress. And because the robustness of math transcends the notorious untrustworthiness of human minds, it seems to have a reality that goes beyond it's creation coming from the minds of men:

Yet, there is something important to be gained in regarding mathematical structures as having a reality of their own. For our individual minds are notoriously imprecise, unreliable, and inconsistent in their judgements. The precision, reliability,  and consistency that are required by our scientific theories demand something beyond any one of our individual (untrustworthy) minds. In mathematics, we find a far greater robustness than can be located in any particular mind. Does this not point to something outside ourselves, with a reality that lies beyond what each individual can achieve?...

He then says a typical critique is that math is just a product of human minds but has these amazing properties because it has been distilled down over years to those human ideas that can consistently be shown to be true by all. He then says this line of reasoning is circular because for everyone to agree that something is right requires an external standard. (Leading us back to an external objective existence.) He then says:

Mathematics itself indeed seems to have a robustness that goes far beyond what any individual mathematician is capable of perceiving. Those who work in this subject, whether they are actively engaged in mathematical research or just using results that have been obtained by others, usually feel that they are merely explorers in a world that lies far beyond themselves--a world which possesses an objectivity that transcends mere opinion, be that opinion their own or the surmise of others, no matter how expert those others might be.

He then decides to illustrate how we might expect history to be different if math was subjective. Fermat's last theorem was proposed as being true 350 years before it was proven. If the theorem was subjective and culturally relativistic, then over 350 years with so many cultures contemplating the idea, surely a counterexample may have been constructed. Back to Penrose:

Let me illustrate this issue by considering one famous example of a mathematical truth, and relate it to the question of 'objectivity'. In 1637, Pierre de Fermat made his famous assertion now known as 'Fermat's Last Theorem.'... Fermat's mathematical assertion remained unconfirmed for over 350 years, despite concerted efforts by numerous outstanding mathematicians. A proof was finally published in 1995...

Now, do we take the view that Fermat's assertion was always true, long before Fermat actually made it, or is its validity a purely cultural matter, dependent upon whatever might be the subjective standards of the community of human mathematicians? Let us try to suppose that the validity of the Fermat assertion is in fact a subjective matter. Then it would not be an absurdity for some other mathematician X to have come up with an actual and specific counter-example to the Fermat assertion, so long as X had done this before the date of 1995...

I think that virtually all mathematicians, irrespective of their professed attitudes to 'Platonism', would regard such possibilities as patently absurd.

In conclusion: Just because humans discovered something, like math, doesn't mean they invented its  objective reality. Belief in such an objective existence independent of the minds of men leads one to be able to "feel that they are merely explorers in a world that lies far beyond themselves--a world which possesses an objectivity that transcends mere opinion." A world, as Penrose describes later, that seems to transcend time and this mortal sphere as it seems to be vastly larger then what is needed to describe this physical world and in fact would be largely unknown if we tried to limit math to that which does seem applicable to this mortal sphere. And as Penrose alludes to in the first quote, if the existence of an objective mathematics beyond the minds of men actually exists, what what other such objective frameworks my exist in reality?  I will let the readers decide for themselves but the possibility of exploring such timeless and objective "worlds that [lie] beyond ourselves" to me is fascinating.

How Science-Ready Are the Kids?

As a teacher of intro astronomy here at CU, I have the privilege of seeing the math and science readiness of some of the best and brightest Colorado has to offer the world.  While many of my students struggle with things like unit conversion and basic algebra, many are also able to apply calculus and even differential equations to astrophysical problems. So how science-ready are Coloradans? From the very smart folks at the AIP's Statistical Research Center, the answer is a resounding "average".

I'm really glad I'm not teaching intro astronomy in Mississippi.

Looking at the map, it looks surprisingly similar to another map I recently saw of the distribution of minority populations in the US.

With the exception of West Virginia and Nebraska, all of the other states that rate "Far Below Average" or worse have large minority populations, and all of the states that rate "Far Above Average" except New York don't. 

Additionally, another map looks pretty similar too, this one of the average income per household.

With the exception of California and Nevada (note that this is 2008 data so the full impact of the recession hasn't been included), all of the under-preforming states are green or blue, while all of the over-achievers are yellow or red, with the exception of Indiana and Maine.

Fixing Math

An OpEd piece in the New York Times this morning made a very interesting proposition on how to teach high school math.  From the article:

Imagine replacing the sequence of algebra, geometry and calculus with a sequence of finance, data and basic engineering. In the finance course, students would learn the exponential function, use formulas in spreadsheets and study the budgets of people, companies and governments. In the data course, students would gather their own data sets and learn how, in fields as diverse as sports and medicine, larger samples give better estimates of averages. In the basic engineering course, students would learn the workings of engines, sound waves, TV signals and computers. Science and math were originally discovered together, and they are best learned together now.

As people who use math as a tool to do science, I wanted to get your thoughts on this idea.  May I propose two questions:

1. One of the benefits of learning math is an ability to think abstractly rather than simply act as a calculator.  Does teaching math in an applied context hurt the student's ability to think abstractly?
2. In your experience, do high school math teachers have the technical background to effectively teach those courses?

Should Bayesian Statistics Decide What Scientific Theory Is Correct?

Bayesian statistics is used frequently (no pun intended for our frequentist friends) to rule between scientific theories.  Why?  Because in a laymen nutshell, what Bayesian statistics does is tell you how likely your theory is given the data you have observed.

But a question arises: should we feel comfortable accepting one theory over another merely because it is more likely than the alternative?  Technically the other may still be correct, just less likely.

And furthermore: what should be the threshold for when we say a theory is unlikely enough that it is ruled out?  The particle physics community has agreed at the 5σ level which is a fancy pants way of saying essentially the theory has a 99.9999426697% chance of being wrong.  Is this too high, too low or just right?

The Inverse Problem: For an example lets assume that supersymmetry (SUSY) is correct and several SUSY particles are observed at the LHC.  Now, it seems like there are 5 bajillion SUSY models that can explain the same set of data.  For example, I coauthored a paper on SUSY where we showed that for a certain SUSY model, a wide variety of next-to-lightest SUSY particles are possible.  (See plot above).  Furthermore, other SUSY models can allow for these same particles.

So, how do we decide between this plethora of models given many of them can find a way to account for the same data?  I am calling this the inverse problem: the problem where many theories allow for the same data so given that data how can you know what theory is correct?

Back to Statistics: Well, for better or for worse we may have to turn to Bayesian statistics.  As already discussed, Bayesian statistics can tell us which theory is more likely given the data.   And knowing what theory is more or less likely may be all we have to go off of in some cases.

So again I will ask: should we really be choosing between two theories that can reproduce the same data but one has an easier time doing it than another?  Is this just a sophisticated application of Ockham's razor?  Should we as scientists say "The LHC has shown this theory X to be true" when in reality theory Y could technically also be true but is just far less likely?

What do you think?

The Wonder of Mathemagic. (Insane what some people can do!)

This video from TED demonstrates how well some people can do math in their head. It is really worth watching and is truly frighting!

That said, if you watch you will realize what he is doing just further illustrates that many patterns exist in and between numbers.  Number theory is quite a remarkable subject! And some people are just really clever at coming up with some interesting algorithms.

Math Quote Of The Day. (Gödel's Second Incompleteness Theorem)

Wolfram stating Gödel's second incompleteness theorem informally:

Any formal system that is interesting enough to formulate its own consistency can prove its own consistency iff it is inconsistent.

The iff isn't a misspelling, it means "if and only if" for those who may not know.

I love this theorem, a source of such great philosophizing. :)

Simple Math: You Fix the Deficit

Raise your hand if you like the idea of a balanced federal budget.  Now keep your hand up if you actually have some idea of what it would take to achieve a balanced federal budget.  When nearly 15% of what the federal government spends is coming from borrowing it's very hard to actually figure out where one might come up with half a trillion dollars or so to close the gap.

The New York Times has come out with an online deficit-reduction form which allows you to pick and choose among dozens of measures designed to increase tax revenue or slash spending in order to get the federal government to stop spending more than it brings in.  I suggest playing with it to see just what it's going to take to get budget balanced.

The funny thing to me is that this is really extremely simple math (TAXES - SPENDING = 0) however it seems to be somewhat more complicated in practice than in theory.  This is one reason why I am a theorist.

Are You Ready To Find the Love of Your Academic Life?

Everyone who has watched TV has seen commercials for websites like eHarmony.com or match.com which promise to use some-sort of scientific algorithm to help you find your ideal man or woman.  They show happy couples gushing about how perfect they are for each other and how they never would have found each other without this website's proven deep-compatibility matching.  My favorite fictional physicist, the great Sheldon Cooper, calls this "unsupportable mathematics designed to prey upon the gullible and the lonely".

Now unsupportable mathematics are being applied to something eerily similar to dating - college admissions.  The website WiseChoice.com claims to be "your personalized path to college" by using algorithms modeled on those of eHarmony to match prospective college students with colleges that match their academic, social, and career preferences.  One New York Times' writer called it "self-discovery through test taking".  Using a series of questionnaires designed to measure things like study skills, preferred social setting, desired level of independence, inclination towards religious institutions, and the relative importance of things like school- and class-size, WiseChoice computes a"match percentage" designed to measure how well you would fit in at each school.  Additionally, if you give them things like your high school GPA and test scores they will sort your top matches into three categories - "reach", "target", and "safety".

So I thought I'd try it.  I entered my data into the site as if I were today exactly as I was when I was applying for college 10 years ago. Here are my top matches from each category:

Reach Schools

My top reach schools were rated as Harvard and MIT, both 85% matches.  I applied to both for grad school and can confirm that they were a bit of a reach for me.

Target Schools

The schools I apparently should have been applying to were Notre Dame and College of the Ozarks.  College of the Ozarks, my highest overall match, was especially interesting as it is a non-denominational Christian private school that charges no tuition in exchange for all students working 15 hours per week on campus during the school year and two 40-hour weeks during either winter or summer break.  I never even considered applying to either of these schools, but it's starting to become apparent that WiseChoice picked up on my preference for a religious institution.

Safety Schools

My top safety school resulted in a three-way tie between College of the Holy Cross, Faulkner University, and Wake Forest.  All three of these are religious schools affiliated with the Catholic Church, Church of Christ, and Southeastern Baptist Conference, respectively.

So how does that compare with the colleges I actually considered as a high school senior?  Back then I was thinking about a lot of places but there were really four favorites.  BYU was the clear front-runner as I had been born in Provo while both of my parents were students there.  Stanford was my "reach" school.  The University of Oregon was my "safety" school. My last school was sort of an odd-ball pick that was mostly my feeble attempt at doing something no one expected me to do, and that was apply to Washington University in St. Louis.  Here's what WiseChoice thought of those 4 schools.

BYU was rated a safety school with an extremely high match percentage.  Stanford and Washington U. just missed the cut as reach schools as WiseChoice's lowest recommendation for a reach school was Dartmouth with 83%.  And the University of Oregon is apparently so far below my standards that it was rated "extreme safety".

So does this thing really work?  It picked up on my pro-religious school preference but not on which religion I preferred.  It really didn't pick up on my desire not to sell my internal organs to pay tuition as some of my top matches were extremely pricey.  It also had no qualms suggesting several small schools that I had never heard of before, even though I wanted a larger school.  So my final verdict is that while it's interesting to see the results, it really is based on "unsupportable mathematics".

What's Your Favorite Math Equation And Why?

Back in 2004, Physics World polled their readers asking what was the greatest math equation ever?  As Joseph Polchinski has recently noted:

[They] came up with a two-way tie between Maxwell’s equations

and Euler’s equation

The remarkable appeal of Euler’s equation is that it contains in such a compact form the five most important numbers, 0,1,i,π,e, and the three basic operations, +,×, ˆ. But my own choice would have been Maldacena’s equation

                                         AdS = CFT

because this contains all the central concepts of fundamental physics: Maxwell’s equations, to start with, and their non-Abelian extension, plus the Dirac and Klein-Gordon equations, quantum mechanics, quantum field theory and general relativity.

All good equations and I must say I stand in awe of how much symmetry, beauty, and information they pack into one line.

That said, my favorite equation is Stokes Theorem written in the full differential forms machinery:

Look how symmetric!  This equation both generalizes the fundamental theorem of calculus and illuminates the heart of the duality between homology and cohomology groups in algebraic topology.

Now, please share your own equations and why you like them!  I'm interested in what your favorite equations are, whether you enjoy them for technical reasons or not.  Even if your equation is something like:

One egg + one cup of sugar + one cup of peanut butter + 10 minutes at 350 degrees = a surprisingly good set of peanut butter cookies.

Please share.

Do We Teach Any Math in High School?

I am currently working to install pavers on the back patio of my home.  The previous owner had installed pavers without properly preparing the soil underneath, which caused the pavers to settle and become uneven over time.  To prevent this I have had to rip up the pavers and dig out a couple inches of the Devil's own soil, otherwise known as clay.  Next I will have to fill in the missing clay with coarse gravel (3/4" road base to be specific) and then re-lay the pavers.  Such are the joys of home-ownership.

This morning I called the local sand and gravel company to order the 20 cubic feet of gravel that I need to complete the next step of my project.  What follows is the conversation (as best I can reconstruct it) I had with Jim, the guy that takes phone orders for this company. 

Me:  I'd like to order 20 cubic feet of 3/4" road base please.
Jim:  I'm sorry, how many square feet do you want?
Me: I want 20 cubic feet.
Jim: We only sell in square feet.
I'm sorry, I want a volume of gravel, so I think that should be measured in cubic feet.
Well we only do square feet, like I said.
Ok, I'd like a volume of 3/4" road base that's 20 square feet across the top and 1 foot thick.
Our minimum order size is 100 square feet.
Ok, let's try this - how much does 100 square feet of 3/4" road base weigh?
I don't know. Let me ask somebody. (Puts me on hold for a couple minutes). Okay, sorry about that. 200 square feet of road base weighs 1 ton.
And how thick is that layer of road base spread over 200 square feet?
2"
(Pause for some quick math) Ok, then I want 128 square feet of 3/4" road base.

That's right - I ordered a volume of gravel in 2-D.  My 128 square feet of gravel will be delivered between 9 AM and 11 AM tomorrow morning.  I weep for the future.

(Note:  I originally wrote the I ordered 228 square feet in this post.  After several intelligent comments pointing out that I would have ordered far too much gravel that way, I went back and checked my order and I did, in fact, order "128 square feet" of road base.)

Math Quote Of The Day.

Having discussed the axiom of choice earlier today I wanted to post a quote by the mathematician Jerry Bona.

"The Axiom of Choice is obviously true, the well-ordering principle obviously false, and who can tell about Zorn's lemma?"

I guarantee you mathematicians will find this hilarious but for those of you left in the dark, the Wikipedia goes on to say:  "This is a joke: although the three are all mathematically equivalent, many mathematicians find the axiom of choice to be intuitive, the well-ordering principle to be counterintuitive, and Zorn's lemma to be too complex for any intuition."

Math Quote Of The Day.

From the mathematician Yuri Manin quoted here:

A proof only becomes a proof after the social act of “accepting it as a proof".

Unfortunately, there is some truth to this.

The Eternal Universe Welcomes Keith Penrod!

We at The Eternal Universe are proud to welcome Keith Penrod as a coauthor.  Keith has a BS and MS in Mathematics from Brigham Young University. His hobbies include doing math, thinking about math, geeking out about math, and mathing.

He is currently working on his PhD in math at the University of Tennessee-Knoxville. He specializes in pure mathematics. (Ie... the important stuff like topology.) He plans to be a mathematics professor, probably somewhere in the West close to home.  Though he may not admit it, he is one of the finest mathematical minds we know.

Occasionally his good friends convince him that there's more to life than math, namely real life itself. While physics is not one of his strongest areas, he does have interest there and is honored to be on the blogging team.

If these images don't make sense, I apologize; just know they should be hilarious to those looking at science from Keith's perspective.  Much like this post should.

Last joke:  You know you are a topologist when, after seeing a drunk person flopping around muttering a string of four letters words, your first thought is: did he just triangulate the 2-sphere?

Welcome Keith!

How Not To Do Basic Math. (Hilarious)

The videos below are classic.  Does anybody else notice that standard notation for division has changed over the years?

Are Physical Theories Just Models?

Look at the figure to the right.  There is a physical world which we observe.  From these observations we derive physical laws.  (Usually expressed in mathematical statements).  A question arises: Is the universe really obeying these laws or did we just get lucky in finding something that models the behavior we observe? 

Moreover, can we ever know?

Here is a similar thought by Peter Szekeres:

When we consider the significant achievements of mathematical physics, one can not help but wonder why the workings of the universe are expressible at all by rigid mathematical 'laws'. Furthermore, how is it that purely human constructs refined over centuries of thought, have any relevance at all?... Some of these questions and challenges may be fundamentally unanswerable, but the fact remains that mathematics seems to be the correct path to understanding the physical world.

Though the above is philosophical, I think it is still worth pondering. 

To Me It's Okay Because The Models Have Predictive Power.

Even if physical theories are no more than models, I still find the pursuit of science very valuable because of its predictive power.  Models or not, modern scientific theories predict masses, velocities, positions, charges...  From these predictions we can create electronics, build cities, cure diseases, etc...

Science therefore does not suffer from the same thing that plagues many other philosophical constructs. For example, from Steven Weinberg:

Why was Aristotle... satisfied with a theory of motion that did not provide any way of predicting where a projectile or other falling body would be at any moment during its flight...? According to Aristotle, substances tend to move to their natural positions... but Aristotle did not try to say how fast a bit of earth drops downward or a spark flies upward. I am not asking why Aristotle had not discovered Newton's laws... 

What puzzles me is why Aristotle expressed no dissatisfaction that he had not learned how to calculate the positions of projectiles at each moment along their paths. He did not seem to realize that this was a problem that anyone ought to solve. 

Even if physical theories are only models of reality, with modern science we have real predictive power so Aristotle's problem no longer exists and I believe this is a wonderful thing.

Michael Dine: Do Symmetries Exist At High Energies?

In our last post on Hořava-Lifshitz gravity we discussed a theory where a symmetry, Lorentz invariance, may not exist on small scales (high energies) even though it does on large scales (low energies).

I attended a talk by Michel Dine which was given at UC Irvine a while ago.  He made a remarkable claim: He said that he had some back-of-the-envelope type calculation that led him to believe the number of possible theories where the low energy symmetries vanish at high energies is much much larger that the number of theories where the low energy symmetries hold at high energies.

He took this idea to speculate that maybe we are fooling ourselves trying to work on theories where our low energy symmetries hold at high energies.   He didn't say this but this made me wonder: maybe Hořava is on a smart track.  Maybe his gravity theory is wrong but maybe more people should consider theories where the symmetries we know and love at low energies do not hold at high energies.

Now, I'm sure demanding symmetries to hold at high energies is the safest thing to assume.  Still, it just may be that our low energy symmetries are all violated at high energies.

Ed Witten On The Definition Of A Quantum Theory.

Here is an example of why Edward Witten seems to be on a different intellectual plane from the rest of humanity.

He has some lectures on quantum field theory online.  I decided it may be fun to read some of them since: it's Ed Witten!  On lecture one he decides to define what he means by a quantum theory:

We will define a quantum theory to be a pair (A,H) where A is a *-algebra (not necessarily commutative), and H is a selfadjoint element of A, defined up to a real number.  The algebra A is called the algebra of quantum observables (operators),  The element H, as before, is called the Hamiltonian...

By a realization (or solution) of a quantum theory (A,H) we will mean an irreducible *-representation of the algebra A in some Hilbert space H, such that the spectrum of the operator H is bounded from below (representations are considered up to an isomorphism that preserves H).  We will always normalize H so that the lowest point of a spectrum is zero. 

Now, it turns out if you have taken enough math, quantum mechanics and read through the above slowly you can see that what he is saying does make sense. (Obviously, as if he would be wrong.)

But come on!  I don't think any normal human thinks about quantum principles as deeply and rigorously as this.  Edward Witten is definitely very special and part of me wishes I could understand physics at this level.

The Wonders of Math

This post goes out to anybody who has ever been a TA for GE physics or astronomy, to those who have been asked math questions that reveal a profound lack of understanding. My wife found this little pictorial story online and it needs to be shared with those of you that will appreciate it.

Doing Math In Your Head

Some of us have impressed others which the kind of math we can carry out in our head.  However, this guy takes the cake.

Just How Pretty/Ugly Is The Standard Model?

Sorry this post contains equations.  (I had treat myself and make such a post at some point.)

The standard model is the creative name physicists have given to the theory that successfully unites the three forces: electromagnetic, strong and weak forces with all of the known particles but fails to explain gravity.  Excluding gravity, the standard model seems to explain everything we know about the universe with a few modern exceptions such as dark energy and dark matter.

Now, how beautiful is this theory?  In modern physics, theories are derived from "actions".  (Later I will post on why this is.)  When you "extremize" an action, it gives you equations that tell you what exactly your theory is.

For example, here is the entire action for general relativity:

When you "extremize" this action you get everything we know about general relativity. (And hence gravity).  The Einstein equations from such this action become: (Details here.)

This may not be apparent, but all of general relativity follows from such elegant looking equations.  Ah, so beautiful.

Another example is the action that gives rise to Maxwell's Equations, and thus all of electricity and magnetism: (The integral of this quantity is the action)

Here are the Maxwell Equations, derived from the above action, in all their symmetrical glory:

Now let's look at the Action for the standard model.  The action is the integral of this beast: (Click to See.)

Let's just say all of the equations that come from this is just too much.

There you go.  That image contains all the physics we know about the entire universe minus gravity. And now you all know how beautiful/ugly, the standard model is. :)