Three Kinds of Lies: Statistics on BYU Football

I have been fascinated with the quarterback controversy that plagued BYU this season between the hyped phenom Jake Heaps and the grizzly "gamer" Riley Nelson.  While Nelson had much better traditional statistics than Heaps, Heaps played against a tougher schedule. The author of a the BYU sports blog LoyalCougars.com asked me if it were possible to statistically correct for the difficulty of the defenses Heaps and Nelson played to compare them on level ground.  Being a football fan and a math nerd, I dove right in.  The results are written up in a post over at LoyalCougars.com, so if you feel like delving into the statistical rabbit hole, go check it out.

Physics PhDs: How Many? How Long? How Worthwhile?

I regularly sing the praises of the Statistical Research Center at the American Institute of Physics, so forgive me if you've heard this song before.  The latest data release from the SRC has a couple interesting tidbits profiling the newly minted PhDs in physics and astronomy.

First of all, the number of PhDs awarded continued its decade-long rise since the low of the late 90's dot-com boom.  The last time the US produced this many PhDs in physics was the mid-1960's when the space race, the nuclear arms race, and dozen of other defense-related Cold War initiatives drove hoards of students into PhD programs. 

The second interesting tidbit is the distribution of time-to-PhD for recent graduates.  I have seen averages previously, but it's great to see the histogram.  It's clear that the "5-year PhD" model is really a myth more than anything at this point.

Finally, the last tidbit is a fun little question that the AIP asked.

Interestingly only 22% of American students would change anything about their PhD experience while half of non-US citizens would.  Perhaps American are either too proud or too complacent to admit they would have done something different if they had it all to do again.

Should Bayesian Statistics Decide What Scientific Theory Is Correct?

Bayesian statistics is used frequently (no pun intended for our frequentist friends) to rule between scientific theories.  Why?  Because in a laymen nutshell, what Bayesian statistics does is tell you how likely your theory is given the data you have observed.

But a question arises: should we feel comfortable accepting one theory over another merely because it is more likely than the alternative?  Technically the other may still be correct, just less likely.

And furthermore: what should be the threshold for when we say a theory is unlikely enough that it is ruled out?  The particle physics community has agreed at the 5σ level which is a fancy pants way of saying essentially the theory has a 99.9999426697% chance of being wrong.  Is this too high, too low or just right?

The Inverse Problem: For an example lets assume that supersymmetry (SUSY) is correct and several SUSY particles are observed at the LHC.  Now, it seems like there are 5 bajillion SUSY models that can explain the same set of data.  For example, I coauthored a paper on SUSY where we showed that for a certain SUSY model, a wide variety of next-to-lightest SUSY particles are possible.  (See plot above).  Furthermore, other SUSY models can allow for these same particles.

So, how do we decide between this plethora of models given many of them can find a way to account for the same data?  I am calling this the inverse problem: the problem where many theories allow for the same data so given that data how can you know what theory is correct?

Back to Statistics: Well, for better or for worse we may have to turn to Bayesian statistics.  As already discussed, Bayesian statistics can tell us which theory is more likely given the data.   And knowing what theory is more or less likely may be all we have to go off of in some cases.

So again I will ask: should we really be choosing between two theories that can reproduce the same data but one has an easier time doing it than another?  Is this just a sophisticated application of Ockham's razor?  Should we as scientists say "The LHC has shown this theory X to be true" when in reality theory Y could technically also be true but is just far less likely?

What do you think?

The Statistical Mechanics of Money

Yesterday I listened to a talk by Victor Yakovenko of the University of Maryland about the physics of money and it was quite interesting. I think that after this talk I am finally beginning to understand economics while at the same time I suspect that most economists don't.

In his talk he said that back in 2000 he published a paper on how to apply statistical mechanics to free market economics. He did it as a hobby and did not consider it to be very important, meaning he still did his normal research involving condensed matter physics. A few years later he realized that his paper on the statistical mechanics of money was getting more citations than any of his other papers, so he switched his focus of research to Econophysics.

One of the most interesting results that he found was that in a free (random) system of monetary exchanges the natural distribution of money will converge, over time, on a Boltzmann-Gibbs distribution. The argument is simple. In stat mech you have a system where small, discreet amounts of energy are passed from one particle to another. This system leads to a probability distribution characterized by the equation [all images come from Dr. Yakovenko unless otherwise stated]:

Where we have the probability of finding a particle at a particular energy level on the left and the energy, represented by ε, and temperature on the right. If we change the energy to money (or income) and temperature to average income we have:

So what does this mean in reality? Well consider a system where everyone is given $10 to start out and they can engage in economic transactions worth $1 each (they can either pay $1 or receive $1 per transaction), with the requirement that if anyone reaches $0 they can no longer pay money (i.e. they can't go into debt) but they can receive money, it's just that the other person does not receive money in return (think of it as work done). Over time this system moves to maximum entropy and achieves a Boltzmann-Gibbs distribution. An undergrad at Caltech named Justin Chen, who worked with Dr. Yakovenko, made an animation of this system [you can find more information on this animation here]:

As we see, the system starts out as a delta function but changes to a Gaussian distribution, but because of the hard boundary at m=0 (think of it as the ground state) we end up with a Boltzmann distribution. So as soon as they thought about this they started to look into other things, such as allowing for debt, taxes, and interest on the debt (this is of course assuming conservation of money). When they allowed for debt, but only down to a certain level (i.e. the ground state was shifted to a negative value), they found that it did not change the shape of the distribution but it did raise the temperature of the money (raised the average money).

The way this works is that every time someone goes into debt (negative money) an equivalent amount of positive money is created. Thus while the total amount of money has not changed, the amount of positive money goes up, raising the temperature and thus creating the illusion that there is more money. While this does put some people into debt, it does raise the number of people with more money, thus it makes more people rich (note: the rich do get richer under this system, but the main effect is that there are more rich people. So it is not just that the same people get richer because of the debt, it's that more people have more money). But you may say that this is not very physical because in the real world there is no low limit of debt. In theory someone could have infinite debt (infinite in the sense of very, very large). And in their models, if they remove the debt floor they have precisely this effect, the number of people who go into deep debt grows until we have a flat line fore the distribution.

This problem was solved in 2005 by Xi, Ding and Wang when they considered the effect of the Required Reserve Ratio (RRR), which to explain simply limits the amount of money that lenders can lend. In terms of the simulations this means that every time someone goes into debt the corresponding positive money that is created cannot all be used to finance more debt. A certain amount must be held in reserve. This limits the total debt that can be issued by the system based on the total amount of money that was in the system to begin with. The end effect is that the distribution becomes something like this [From Xi, Ding and Wang]:

This effectively creates a double exponential distribution that is centered about the average money amount. Now we can start to look at some of the effects that things like taxes and interest have on this system. First, interest. If we add interest the system does not have a stable state and without any form of check the system will expand to infinity, in both directions. Second, taxes. Assuming a tax on all transactions, either a fixed amount or a percentage, and then assuming the tax is then evenly redistributed, this will shift the peak slightly to the right, though it will not change the edges that much. So a redistributive tax will raise the income of people near 0 slightly, away from 0, but it will have very little effect on the overall shape or the edges (the very rich or the most indebted). If we allow for bankruptcies then that acts as a stabilizing force on the system, that is, it keeps it from spreading to infinity. Thus interest creates no stationary state, but bankruptcy creates a stable state. He noted that what the Fed is currently doing is in response to the economic crisis, the negative end of the money (the debt) has shrunk considerably because of foreclosures, and other problems, but to keep the positive end from shrinking as well they pumped more money into the system to maintain the size and shape of the distribution. While this does prevent the positive side from collapsing, the trade off is that there is more money put into the system, creating the potential of inflation. (As a side note: part of the reason we got into this mess in the first place is because banks found a way around the RRR requirement, allowing them to issue more debt than they should have, which gave the impression that the economy was booming because there was more positive money, but this ignored the fact that there was a corresponding amount of debt being created. The debt was limited by personal bankruptcy and thus created a domino effect that removed both the debt, but also a significant amount of the positive money. We have yet to even come close to recovering to the level we were at before. If you hear talk about the Fed keeping interest rates low to spur lending, they are trying to create more positive money through lending, by creating negative money, but because that is not working they have begun printing more money (buying government bonds) to create more positive money without having to create more negative money.)

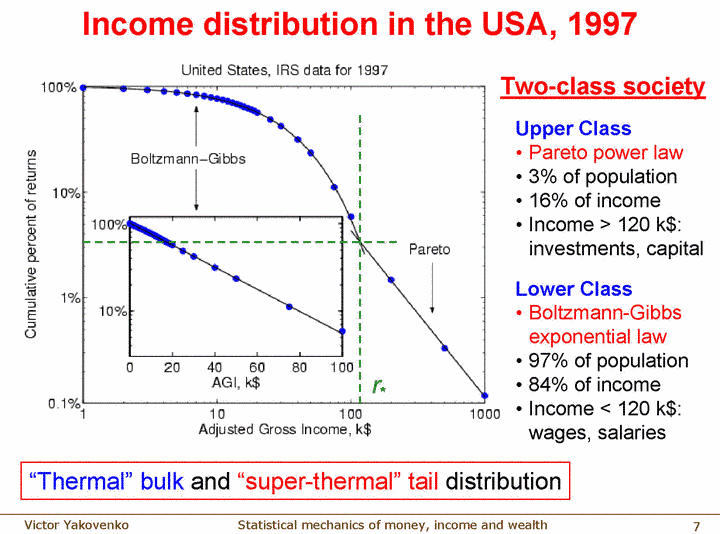
Now let's look at some real data. Using US census data from 1996 they plotted income and found that it fits nicely to a Boltzmann distribution, as long at you do not get too close to $0 (above $10,000 works fine).

But this only works up to a point. They found that up to some point the income of people fits very nicely to a Boltzmann Distribution but above a certain point income behaves differently. If you plot all they way up into the highest levels of income you see a clear point where the income changes from Boltzmann-Gibbs to a Pareto power law distribution.

They noted that while the lower Boltzmann distribution does not change much over the years, despite recessions and boom times, the top "super-thermal" tail changes a lot depending on the economy. This super-thermal tail represents only 3% of the people, but holds anywhere between 10-20% of the money. The total amount of the inequality depends on the economy at the time.

So what happens when this distribution gets upset by programs such as social welfare or other effects. In a paper published in 2006, Banerjee, Yakovenko, and Di Matteo give the following graph showing the distribution of income in Australia.

The spike on the lower end is the welfare limit. People below this limit are brought up to the limit though welfare, but people just above it are also brought down to the level because of taxes. Hence the spike but also the dips on both sides. The result is more equality, but at the expense of lowering the entropy of the system and creating this deviation from the normal distribution. The desirability of doing something like this is debatable (as one professor asked after the talk, "What's wrong with inequality?")

When asked about the predictive power of this his response was, "None." He explained that this data takes a long time to collect and to analyze, which creates a lag of several years in the data. But by the time the data has been collected and analyzed and we are able to see a bubble (like the housing bubble) the bubble has already burst and we have moved on. But this also means that modern free market economics behaves in a very statistical manner and can thus be controlled (in theory), which is what the Fed is currently trying to do. Dr. Yakovenko did not get too much into the politics of it, but he did make it clear that he did not agree with the way the bailouts were handled, and the current tactic of the Fed. But it was also clear that he preferred a free market, though a heavily regulated one. He was also very concerned about the inequality in the system, and noted the existence of two classes of people and made reference to Karl Marx at that point.

On the whole I was rather impressed with what he was doing and like I said, I think I am finally beginning to understand economics. Someone just had to explain it to me in terms of physics and it made perfect sense.

XI, N., DING, N., & WANG, Y. (2005). How required reserve ratio affects distribution and velocity of money☆ Physica A: Statistical Mechanics and its Applications, 357 (3-4), 543-555 DOI: 10.1016/j.physa.2005.04.014

Statistics with No Error Bars or Systematics.

I had someone try to convince me something recently using several statistics with no error bars attached or discussion of how they were obtained, any known systematics and how they were addressed, etc...   This seems to be a common practice among most people (my claim with no firm statistic cited :) )  and reminds me of this:



I'd be interested, for example, if the world would be any different if advertising campaigns were forced to attach error bars and descriptions of their systematics when quoting statistics.

(Although, admittedly, life and especially casual conversations, wouldn't be as fun if they had to be rigorous all the time.)

Thoughts?

Distinguishing Our Universe From Other Similar Universes In The Multiverse.

Srednicki and Hartle have raised an interesting concern recently about a limitation on the predictive power of multiverse theories. They observe that in multiverse theories, exact snapshots of our universe happen several times in different places. So if we want to have a physical theory that describes our universe, the one we live in, then the question arises: how can we tell which one it is from all the others?

From the paper:

Theories of our universe are tested using the data that we acquire. When calculating predictions, we customarily make an implicit assumption that our data D₀ occur at a unique location in spacetime. However, there is a quantum probability for these data to exist in any spacetime volume. This probability is extremely small in the observable part of the universe. However, in the large (or infinite) universes considered in contemporary cosmology, the following predictions often hold. 

• The probability is near unity that our data D₀ exist somewhere. 

• The probability is near unity that our data D₀ is exactly replicated elsewhere many times.  An assumption that we are unique is then false.

This paper is concerned with the implications of these two statements for science in a very large universe... 

The possibility that our data may be replicated exactly elsewhere in a very large universe profoundly affects the way science must be done.

In order to solve this problem, the authors propose creating a "xerographic distribution" ξ.  Given the set X of all the similar copies of our universe in the multiverse, this xerographic distribution ξ gives a probability that we are the specific snapsot X_i of that set.

The authors claim that this distribution cannot be derived from the fundamental theory.  The fundamental theory can only predict the structure of the whole universe at large, not which snapshot in it we happen to be.  However, given a certain ξ, we can use Bayes Theorem to test which ξ appears to be most correct, and once that ξ is established, we have now a statistical likelihood hinting at which universe in the whole multiverse is ours.

So, given a fundamental physical theory T and a xerographic distribution ξ, the authors say:

We therefore consider applying the Bayes schema to frameworks (T,ξ). This involves the following elements: First, prior probabilities P(T,ξ) must be chosen for the different frameworks. Next, the... likelihoods P^(1p)(D₀|T,ξ) must be computed. Finally, the... posterior probabilities are given by

The larger these are, the more favored are the corresponding framework.

The authors then go on to give some examples of how this might work and solve issues with Boltzman Brains etc...

So, just to repeat:

1. One glaring problem with multiverse theories is our universe happens several times in several places throughout the multiverse.
2. However, we would like a good physical theory to make predictions about the snapshot we happen to live on.
3. The fundamental theory of the multiverse cannot tell us which snapshot we are.
4. However, creating a xerographic distribution ξ we may be able to put probability estimates of which copy is ours using Bayes Theorem.

Some further thoughts and Questions.  I remind the readers, as crazy of a topic this paper covers, it did get published in a respectable journal: Physical Review D.  However, while reading the paper I had several thoughts come to mind and I would appreciate your own thoughts on these issues:

1. How should we feel about multiverse theories given issues like this arise?
2. Can only tenured professors get away with writing such articles?  IE... if a grad student wrote papers like these will universities take him/her seriously when applying for a faculty position?
3. What is your "exact other" in the "other snapshots" doing right now? :) 

Srednicki, M., & Hartle, J. (2010). Science in a very large universe Physical Review D, 81 (12) DOI: 10.1103/PhysRevD.81.123524

Random Basketball Shooting (Explains High Nerd Score)

Today, after enjoying watching the Lakers go up 3-0 on the Jazz, I decided to go to the gym.  At UC Irvine, we have a nice track that borders a few basketball courts.  While running around the track, I watched the players miss some pretty lousy shots.

Anyways, I began wondering how often you would make a basket if you literally shot randomly.  I decided I had to know the answer so I went home and wrote a Monte Carlo code (in Python of course).  (Now I know why I got such a high nerd score.)

Here is the code:

As you can see from the code I put a player on a random spot on the floor from which he/she shoots a random shot.   I used this to get the details of the court size.  The units are in feet except the angle of the shot which is in radians.

I assume that the average random shot a person would make would have the distance of a typical "free throw" shot as it passes the the "10 foot plane" the rim sits at with a standard deviation of half that distance.    Furthermore, I don't take into account the advantage of the backboard or the infrequent shot off the wall into the rim.  However, this is deficiency (hopefully) is compensated by the rim being square instead of round (and therefore having more surface area) plus not allowing ball to "bounce out".

I then ran this code 100 times to get an error estimate.

And here is the results:  If you were to randomly shoot a ball in a basketball court a million times you should expect to make 681 +/- 26 (0.068%) out of the million in either basket and 342 +/- 19 (0.034%) in your own basket.

Therefore, if you are playing basketball and are not making ~ one out of every 1468 (unblocked) shots, (in either basket) there is something really wrong with you.  

Watch for Falling Ice

Myth: 4 Russians die from falling icicles every year.
Fact: 5 Russians die from falling icicles every year.

From the Associated Press story entitled "Killer Icicles Terrorize Russians":

"Walking along a Saint Petersburg Street immersed in music, Milana Kashtanova, became the latest victim of falling icicles and ice blocks that have killed five people and injured 147 in the city following Russia's coldest winter in 30 years... [D]uring Russia's springtime thaw, residents are forced to run the gauntlet of snapping icicles and blocks of ice falling unexpectedly from roofs, as well as the ground-level hazards of slippery slush and puddles."

This just goes to show you that if you have enough opportunities, events with extremely small (but non-zero) probabilities can happen.

**************************

For those fans of the Office out there, my intro was inspired by Michael Scott's comments on the dangers of rabies, which you can listen to below.

Myth and fact about rabies sound bite The Office (US) sound bites

Statistics on Grad School and Getting a Job

When I (someday) graduate from CU and receive my doctorate, I will be the first person in my family to do so. We have had a small army of Nelsons with Masters degrees and one law degree that I know of, but as far as I know no one before me has gone for a PhD. Since this career path is something I have never seen in my family, I am always very curious to know more about it. I would like to know things like what kind of job I'm likely to have after I graduate and what the job market is like. I imagine that anybody reading this blog as a grad student or undergrad wants to know the same thing.

To answer these questions, I recommend talking to people who have done it. Their experiences cannot be reduced to data, so get them in verbal form. However, as a physicist, I much prefer looking at data over trying to average people's life-stories. Luckily, the American Institute of Physics has a wealth of statistical information on their website. So here's what I have found by running my own little analysis of their data. All of these conclusions will be drawn from data from 1998 to 2008 (or 2006 in some cases). I used a decade worth of data because I felt it was a good compromise between getting trends that are valid today and giving enough averaging time to make this valid for the next 4-6 years (when I hope to be in the graduating/job finding phase). Here's what I've found (in no particular order):

1. For physics PhD programs in the US, on average, per year, there have been 2,519 incoming students, 12,358 enrolled students, and 1,222 PhDs awarded. If you assume a constant dropout rate per year, that means that it takes on average 7.6 years to graduate, 10.01% of students dropout per year, and on average only half of those who start a PhD program will finish it. Those numbers vary by about plus or minus 10% on any given year, except the graduation time, which varies by plus or minus 2 years.
2. The number of incoming graduate students in American programs is growing by an average of 3.3% per year, while the number graduating is growing by 1.0% per year. By comparison, the percent growth in full-time equivalent (FTE) physics faculty has done the following:In on average, the number of FTE faculty is growing by 0.67% per year for PhD-granting departments, and roughly twice that (1.36% and 1.38%, respectively) for Masters and Bachelors departments. The general trends look like this:

I was thinking about drawing some conclusions, but instead I think I'll let you draw your own. Comment away on what you think this all means.

Only Strange If 1 in Pi Are Like You

I was on the Wikipedia looking for the exact values for various confidence intervals when I saw this for one sigma:

ratio outside CI: 1 / 3.1514871

That looks a lot like this ratio:

1/3.14159265

and in fact agrees better than 1%. This has given me my new rule of thumb:

Attribute X about you is weird if only one in pi people share X with you.

(Number of people that find this post interesting: < 1 in Pi.)

NCAA Championship: A Study in Statistics and Multi-Dimensional Parameter Space

As most of you may have heard UNC won the NCAA Basketball championship yesterday. To some people this came as no surprise as they were favored to win. And considering how they played in the first two rounds it also comes as no surprise. So now here comes the critical question, did they win because they were good or because they were statistically preselected by the NCAA championship committee to win?

Previously I have written on conspiracy theories ranging from a US invasion of Canada to the sudden drop in oil prices last year. So now I present my latest conspiracy theory: UNC was selected to win the NCAA championship at the beginning of of March, if not sooner.

You are probably aware of the fact that computer scientists all over the US spend an inordinate amount of time and effort writing a program that will analyze each team and select who will win each game and thus who will ultimately win the championship. The reasons for this are simple, on the one hand it presents and interesting statistical problem in multi-dimensional parameter space that can be solved. On the other hand it is a good way to make money. If you can write a good program that can predict who will win, then you can bet on that team and make a lot of money. It's the same reason people study the statistics of gambling (in one sense this is studying the statistics of gambling). These people who bet on their team obviously don't want to loose money, so they make sure that their program works best.

Now consider that it isn't just college professors betting on online brackets, but now you are a corporation betting on advertising revenue (ESPN, CBS, NCAA, etc.) but now you are not just trying to predict the outcome of a random event, but rather you are trying to maximize your returns, and you have some influence over these seemingly "random events". So lets say you get your hands on one of these predictive programs that seems to work fairly well, but the bracket and tournament has not been decided yet. You have several teams to choose from, to put into 16 slots. You can also determine how these 16 teams will go into the slots.

So you input the data and you see that team A is good at offense OK at defense and good at free throws. Team B is OK at defense but good at offense and free throws. If these two teams played they would be evenly matched, but team A tends to foul more than team B, thus if they played, team B would be more likely to win. So you look at this multi-dimensional parameter space and while there are a number of variables, they all can be reduced to one variable, the score. This makes it immensely simple. So now you look at team C and see that they are good at offense OK at defense and OK at free throws. Now we see that if team A plays team C, the fact that team A tends to foul no longer matters because team C can't make free throws. Thus if you seed team A against team B, team B is guaranteed to win, but if you seed team A against team C it could go either way and come down to a buzzer shot.

As long as the people organizing the bracket have no personal interest in the matter (i.e. they don't or can't bet, and they don't hold personal feelings towards team B) then they just might do it randomly. But now let us introduce another parameter. The organizers know that if they have team A and team B play, team B will win. They know that if team C and team D play, team D will win. Which means team B will play team D in the next round. If you switch the original bracket, then you may have team C playing either team D or A in the final. Now here's the catch. If you have B and D play in the final you can get more sponsors and you get more money. So if all you care about is revenue from sponsorship then it would be easy to "fix" the bracket in order to maximize your revenue.

As a real example of maximizing revenue. Say you have a football (soccer) championship. Would you want the championship game to be played between Newell's Old Boys and Chaco Forever, or would you want the championship game to be played between Real Madrid and Manchester United? (note: Chaco Forever doesn't even have a Wikipedia page...oh wait! I found it, it was spelled wrong) So how much money could be made either way? If you could affect the outcome, and make a little money would you do it? Especially if it appears for all intents and purposes to be legitimate and random? (But really isn't).

So here is my conspiracy theory, whenever it became obvious that they could organize the bracket so that UNC could win, and that they would maximize their advertising revenue that way, the set the bracket and UNC was guaranteed a win. Looking at the point spread for the entire tournament, it has the appearance of being rigged. Just a thought.

Now for your viewing pleasure: This is the celebration that took place on Franklin Street after the game. This is the corner of Columbia and Franklin Streets, which is about a block from the Physics Department. We also have to drive down Columbia Street every time we go to church, to give you some reference.

Timelapse: Franklin Street after the victory from The Daily Tar Heel on Vimeo.

And another video:

Franklin Street: The Celebration from The Daily Tar Heel on Vimeo.

Statistical Quote of the Day

He uses statistics as a drunken man uses lamp-posts — for support rather than illumination.
-- Andrew Lang

Too Old For Physics Theory?

How old is too old to do serious High Energy Physics? Is it true that most theorists work is done in their twenties and maybe thirties? Here is a Chart from Spires to help us out:
Fact: Half the authors were 32 or younger when they published their famous papers, and the largest group was 29-30.

It appears I will need to get my act together. If I get a PhD in 5-6 years then I will be doing my first postdoc during my "prime." Now I see why they said at the lab: "Work hard as a gradstudent, postdoc and new faculty member because that is when you will do your best physics." Being as most high energy theorists don't get tenure until their late thirties I can now see how true this can be.

Now we have to remember these only list top cited papers. Perhaps people in their post 40's years are publishing the most average cited papers. I don't know.

This is also why I was told go to a grad school where the faculty is young, fresh, and excited. They are the ones getting all the top citations.