A Little More Data on Tuition Inflation

One of my previous posts speculated on the relationship between the availability of student loans and the rising cost of higher education.  Inflation of tuition is a complicated issue, but let me share two more pieces of data on the subject. Both are specific to the University of Colorado, but I feel are at least somewhat representative of the larger picture.

First, state support for higher education has dropped dramatically.  In effect, this transfers the actual cost of higher education from the taxpayers to the students.  You can see the fraction of the state budget devoted to higher ed in Colorado below (click to embiggen). 

In the same time period the average cost of a state-school increased by almost a factor of 4 and the state funding in Colorado dropped by about a factor of 4.

The second piece of data concerns another idea I've heard batted around which is that tuition inflation is being driven by excessive pay for administrators and/or faculty.  CU's provost (the head of the Boulder campus) was paid $389,000 last year, which is a lot of money, but it also comes out to 0.03% of the university's operating expenses for 2012.  You can argue that administrative pay is too high, but it's just not a big enough chunk of the budget to be the cause of tuition hikes.  As for faculty pay, a very unscientific study of the faculty in my department shows that they work on average 55 hours per week and make about 85% of what someone with a comparable level of education and experience makes in the private sector according to PayScale.com.

Again, I don't claim to have all the answers, but I do think it's important to get as much data into this debate as possible.  Thoughts?

Does the Availability of Student Loans Drive Up Tuition?

President Obama was here at CU recently taking some great pictures at a local hang-out and talking about student loans.  I'm not going to get into the political issues around student loan interest rates, but something from the discussion caught my interest - the idea that the availability of student loans has caused tuition to rise.  A survey released today shows that 47% of Americans believe that it has.  Clearly the idea behind making student loans more available is not to drive up the price of tuition but rather increase access to higher education, so if in fact easy access to student loans drives up prices then we have a serious problem.

I don't have an answer to this question, but here are a couple bits of data to mull over from the College Board's Trends in Higher Education reports. First, here is the average inflation-adjusted cost of college tuition relative to 1981. 

The fact that a college education today is somewhere near three times as expensive as it was 30 years ago even when adjusting for inflation is alarming, and the natural call is to find ways to make it more affordable, particularly for low-income families.  Student loans are often touted as ways to help many more students for less than it would cost to simply fund the university directly with state or federal funds.

The second graph shows the inflation-adjusted pool of money available for student grants (in blues) and loans (in reds and oranges) per student over the last decade.

From 2000 to the present, tuition has gone up by about 50% and the total financial aid per student has increased by almost exactly the same percentage from about $9,000 per student to a little over $14,000 per student.

Of course correlation does not imply causation and frankly it may be that the increase in tuition is driving the increased availability of financial aid, not the other way around, but I do find this idea intriguing.  As people that have spent a lot of time at colleges, I'm interested in your thoughts.  Does increased financial aid lead to higher tuition and if so how can the government help keep higher ed affordable?

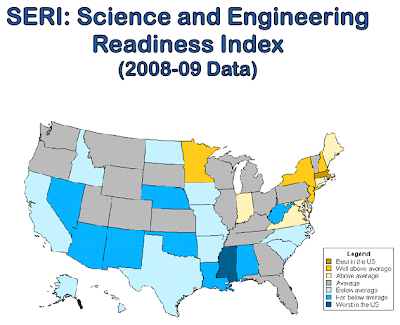
How Science-Ready Are the Kids?

As a teacher of intro astronomy here at CU, I have the privilege of seeing the math and science readiness of some of the best and brightest Colorado has to offer the world.  While many of my students struggle with things like unit conversion and basic algebra, many are also able to apply calculus and even differential equations to astrophysical problems. So how science-ready are Coloradans? From the very smart folks at the AIP's Statistical Research Center, the answer is a resounding "average".

I'm really glad I'm not teaching intro astronomy in Mississippi.

Looking at the map, it looks surprisingly similar to another map I recently saw of the distribution of minority populations in the US.

With the exception of West Virginia and Nebraska, all of the other states that rate "Far Below Average" or worse have large minority populations, and all of the states that rate "Far Above Average" except New York don't. 

Additionally, another map looks pretty similar too, this one of the average income per household.

With the exception of California and Nevada (note that this is 2008 data so the full impact of the recession hasn't been included), all of the under-preforming states are green or blue, while all of the over-achievers are yellow or red, with the exception of Indiana and Maine.

Do Cars and Construction Equipment Discourage Women in Physics?

Physics has a gender problem and to see an example you need look no further than the list of this blog's authors to your left.  You'll note that all of us are male.  A broader look into this problem yields what is known as the "scissors diagram".

Here the black lines show the fraction of men and women at various stages of physics careers while the red lines show the expected fraction from historical trends (because when current full professors were in high school there were far fewer women taking physics than there are today).  It appears that for some reason men and women both take high school physics in nearly equal numbers, but that for some reason women are far less likely to study physics in college.  Physics is not alone in this problem, as I've written about previously, but we are having a much harder time fixing it than fields like math or chemistry.

There are a lot of ideas as to why this might be the case but here's one from a Physics Today article that I hadn't considered before - problem sets based on cars and construction equipment.  I recommend reading the whole article as it is well-written and insightful, but allow me to over-simplify the basic argument:  homework problems in introductory physics courses generally use examples from topics like cars and construction work that are more likely for men to be familiar with than women.

My initial reaction was skepticism - how much difference can using terms like "pile driver" instead of "a machine that drops a heavy weight on [a metal rod], lifts the weight, and drops it again" possibly make?  But the more I think about it, the more I start to think that maybe the authors have a point. I don't think that the real issue is that men are more familiar with pile drivers than women - I think the issue is that when textbook problems appeal more to men than women, a subtle message is sent that women are out of place in physics, and no one wants to feel out of place.

Now don't get me wrong - I'm not arguing that physics problems should avoid real-world examples or that women can't understand problems talking about cars going around banked turns - but I do think it would be wise for physics faculty to try to use more examples from fields that have a higher concentration of women - like health care or preforming arts.  Instead of asking questions about baseball and football only, mix in some questions about ballet.  Ask more questions about blood pressure and less about pneumatic nail guns.  I'm sure this single step won't fix the larger problem, but I think it's generally a good idea to do everything we can to attract the best people to our field and not just the best men.

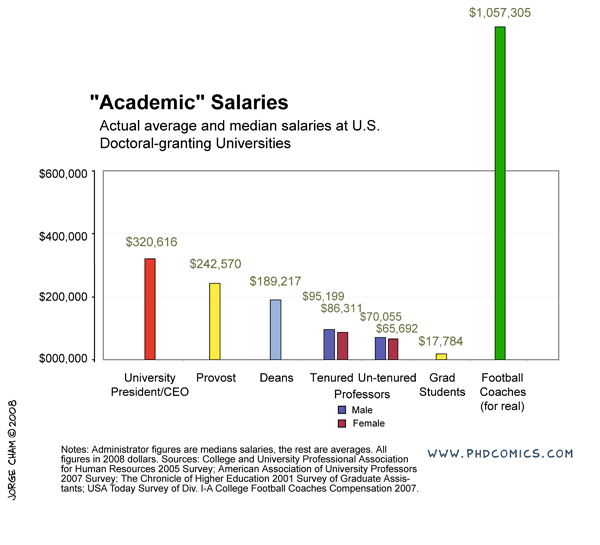
A Good Argument Against Getting an Education

Les Miles (right) is the head football coach at Louisiana State University and the highest paid state employee in the state.  He makes approximately $3,751,000 a year.  He actually said the following at a press conference following his team's win again the University of West Virginia:

There would be a real want, that is, a competing that would happen, which it would, without the need to be compliant or reluctant to not give up that which is the ball, or the things like it, such as the field goals, or even the punt return and defense thereof, and that's keeping the game short and helping the general construction of success as it relates to our football team.

 If there ever was a good argument against education - specifically grammar and basic communication skills - Les Miles is it.

Fixing Math

An OpEd piece in the New York Times this morning made a very interesting proposition on how to teach high school math.  From the article:

Imagine replacing the sequence of algebra, geometry and calculus with a sequence of finance, data and basic engineering. In the finance course, students would learn the exponential function, use formulas in spreadsheets and study the budgets of people, companies and governments. In the data course, students would gather their own data sets and learn how, in fields as diverse as sports and medicine, larger samples give better estimates of averages. In the basic engineering course, students would learn the workings of engines, sound waves, TV signals and computers. Science and math were originally discovered together, and they are best learned together now.

As people who use math as a tool to do science, I wanted to get your thoughts on this idea.  May I propose two questions:

1. One of the benefits of learning math is an ability to think abstractly rather than simply act as a calculator.  Does teaching math in an applied context hurt the student's ability to think abstractly?
2. In your experience, do high school math teachers have the technical background to effectively teach those courses?

More People Like the NRA than the NEA

Since many of us are currently in the business of education and many of us hope teaching will play a significant role in our careers, I thought I would share this interesting piece of social commentary.  From Rasmussen Reports:

A new Rasmussen Reports national telephone survey finds that 42% of all Likely U.S. Voters hold at least a somewhat favorable opinion of the [National Education Association], with 17% Very Favorable. Thirty-seven percent (37%) regard the teacher’s union at least somewhat unfavorably, including 22% with a Very Unfavorable view. Twenty percent (20%) are not sure what they think of the group...Fifty-four percent (54%) of voters view the [National Rifle Association] favorably, including 29% with a Very Favorable opinion. The NRA is regarded unfavorably by 41%, with 25% who have a Very Unfavorable view.

So generally, 12% more of the population likes a group that promotes guns than likes a group that promotes teachers.  While there are clearly other factors (e.g., marketing, political activities, etc.) at work here rather than just a question guns vs. teachers, it made me wonder a little bit about how much society values my aspirations to teach.

Do We Teach Any Math in High School?

I am currently working to install pavers on the back patio of my home.  The previous owner had installed pavers without properly preparing the soil underneath, which caused the pavers to settle and become uneven over time.  To prevent this I have had to rip up the pavers and dig out a couple inches of the Devil's own soil, otherwise known as clay.  Next I will have to fill in the missing clay with coarse gravel (3/4" road base to be specific) and then re-lay the pavers.  Such are the joys of home-ownership.

This morning I called the local sand and gravel company to order the 20 cubic feet of gravel that I need to complete the next step of my project.  What follows is the conversation (as best I can reconstruct it) I had with Jim, the guy that takes phone orders for this company. 

Me:  I'd like to order 20 cubic feet of 3/4" road base please.
Jim:  I'm sorry, how many square feet do you want?
Me: I want 20 cubic feet.
Jim: We only sell in square feet.
I'm sorry, I want a volume of gravel, so I think that should be measured in cubic feet.
Well we only do square feet, like I said.
Ok, I'd like a volume of 3/4" road base that's 20 square feet across the top and 1 foot thick.
Our minimum order size is 100 square feet.
Ok, let's try this - how much does 100 square feet of 3/4" road base weigh?
I don't know. Let me ask somebody. (Puts me on hold for a couple minutes). Okay, sorry about that. 200 square feet of road base weighs 1 ton.
And how thick is that layer of road base spread over 200 square feet?
2"
(Pause for some quick math) Ok, then I want 128 square feet of 3/4" road base.

That's right - I ordered a volume of gravel in 2-D.  My 128 square feet of gravel will be delivered between 9 AM and 11 AM tomorrow morning.  I weep for the future.

(Note:  I originally wrote the I ordered 228 square feet in this post.  After several intelligent comments pointing out that I would have ordered far too much gravel that way, I went back and checked my order and I did, in fact, order "128 square feet" of road base.)

So Exactly Who Is The Smart One Here?

Some days I wonder...

Interesting Plot On Grade Inflation.

The graph above, taken from the blog In The Dark, shows what percentage of students got a grade of A on their A levels.  I believe "A-levels" are exams taken by students who want to go to UK Universities.  From the Wikipedia:

A levels are usually studied over a two year period and are widely recognised around the world, as well as being the standard entry qualification for assessing the suitability of applicants for academic courses in UK universities.

The author of the blog, Peter Coles, has an interesting write up that everyone should really go and read it.  I will just post one snip-it:

Nowadays, on average, about 26 per cent of students taking an A-level get a grade A. When I took mine (in 1981, if you must ask) the fraction getting an A was about 9%. It’s scary to think that I belong to a generation that must be so much less intelligent than the current one. Or could it be – dare I say it? – that A-level examinations might be getting easier?

Looking at the graph makes it clear that something happened around the mid-1980s that initiated an almost linear growth in the percentage of A-grades. I don’t know what will happen when the results come out next week, but it’s a reasonably safe bet that the trend will continue.

I am sure similar grade inflation is happening in the US.  Furthermore, being the younger generation that has benefited from such grade inflation, I can assure Peter our generation is not overwhelmingly more intelligent.

If I was the "grade-czar", I would assign grades based off of standard deviations: A-type grades for +1sigma students, B-type for mean-+1sigma, C-type for -1sigma-mean, D-type for less than -1sigma and F for someone who just wouldn't try or gave up completely.  I would also not accept D credit counting toward graduation.

This way, an A student means the same from one generation to the next: one who repeatedly preforms at a level one standard deviation above his peers.

English Teachers Avert Your Eyes

I'm not a big fan of spelling.  Whoever decided how words are spelled in English was either drunk or sadistic.  As far as I'm concerned spell-checking software is one of the greatest achievements of modern civilization.

That being said, some level of proficiency in written English is really not too much to ask, especially for some words.  From Yahoo!'s news blog:

The thump you just heard is the sound of an English teacher dying of despair.

37% Of The Kids Are Alright

I can, in large part, credit my decision to become a physicist rather than an engineer to my high school physics class.  Prior to that class I thought science was nice, but it all seemed rather fuzzy to me - a lot of hand-waive-y biology and chemistry that was as much about memorization as understanding.  Engineering, on the other hand, was in my young mind much more concrete of a field and certainly heavier on math.  Then I took an algebra-based physics class for the math-impaired and even that was enough to get me hooked.  I saw how physics was simply applying math to the real world and I've been at it ever since.

What I'm trying to get at is the importance of physics at the high school level.  In my obviously biased opinion, physics should be an essential part of high school or - as the Physics First people advocate - the gateway to science education.  So how are we doing?  From the ever-useful folks at the AIP's Statistical Research Center:

While things are looking up compared to the 80's and 90's, only 37% of American high school students take a physics class.  That means that nearly two-thirds of the American public never gets the chance to see the most fundamental science.

So how do we improve that number?  Well one way is to start by working on the states that are bring down the average.

For some reason the inter-mountain west and the southern states seem to be doing the worst, while only 5 states - Michigan, Massachusetts, Texas, Vermont, Wisconsin, and Wyoming - are bringing up the average.  Interestingly, the study notes that requiring more science doesn't equate to more students taking physics:  "two of the lowest physics-taking states did require 4 years of science for graduation, and most of these below average states required 3 years of science".

So if more since doesn't equal more physics, what does?

Creating a Love of Science

As many people in our country have, I have become increasingly concerned with the state of science and mathematics in our educational system, as well as the stigma attached to those who enjoy those subjects. As a result I find myself convinced of the need to inculcate a healthy love for math and science amongst my own children. My wife and I are often on the lookout for good educational games, museums, and opportunities to help our kids in that regard. Additionally, although I surmise that my kids probably don't fully understand my responses, I try to answer their questions as carefully, accurately, and as simply as possible as they relate to the world around us.

Recently, we stumbled across the Hands-On Museum in Ann Arbor, MI. It had been recommended to us by several and we decided to give it a try. In short, it was brilliant! It had many exhibits, each touching on various aspects of "how things work." It had a half-built house showing framing structure, plumbing, heating and air conditioning. It had a biology section showing bone structure, as well as fun cardiovascular and strength exhibits. It had a full-size ambulance available for examination. It had exhibits on sound waves, an optics and light room, a forces and torques section, a pullies exhibit, an automobile section, electricity, and so on. We liked it so much, in fact, that we bought a season pass. Ultimately I'm not sure who liked it more - me or the kids!!

I think it's vitally important to create a sense of wonder and awe for science and nature. There is so much to learn, so many puzzles yet to solve, and so many amazing phenomena, it's hard for me to imagine why anyone wouldn't be interested! So my question, readers, is how do you create this sense of wonderment in your children? Do you have similar museums where you live? Do you spend time with your children talking about nature and how things work?

How Important Is Science Literacy In Society?

Everyone should take six minutes out of their day and watch this video of Neil DeGrasse Tyson speaking on the importance of science literacy at the World Science Festival. (I was pointed to this by Uncertain Principles.)

Here are some highlights I found interesting:

First: Avoiding Self Delusion.

Science literacy empowers you to know when someone is basically full of it...If you understand how the world works, and what the limitations are, then you can judge if someone is trying to exploit your... ignorance.

He gives an example of someone trying to sell you crystals with amazing healing powers.  He argues if you have good science literacy you will know you need to have answered questions such as: "How do they work?  What kinds of ailments do they cure?... How have you tested them?" etc...

Unfortunately, poor scientific literacy may lead to a society that is easily duped and/or will form opinons based on bad ideas.  Those with good science literacy realize the importance for backing up claims, an incredibly important trait as "we as a species are particularly susceptible to self-delusion".

Furthermore, knowing how to test claims should be absolutely crucial for wall street, governments, manufactures and society itself to make correct decisions.

Second: Scientists Understand Liberal Arts, But Often Liberal Artists Don't Understand Science.

Scientists by and large are often quite knowledgeable in areas outside of science.  If you go to the home of most scientists there will be Bach and Beethoven and Shakespeare on the selves...   

One thing I think that as a nation we should be embarrassed by is that the scientists-- you can do this experiment yourself, I've done the experiment-- the scientists, by and large, know more liberal arts than the science that is known by liberal artists."

He then discusses how at a cocktail party of scientists you will never hear them laugh how they never understood how to read Shakespeare or couldn't understand basic nouns and verbs.  However, if you go to a party full of people interested in liberal arts, they have no problem laughing about how they never understood the first thing about math.  Tyson wonders why this causes no embarrasement.

Or as said on Uncertain Princpiles linked above:

It should be exactly as embarrassing in educated company to say "I'm no good at math" as it would be to say "I'm no good at reading."

I'm biased but I think there is a point to be made here.

Thoughts?

Bill Gates Releases Feynman's Lectures For Free

Though I use Linux and think the open source software model is best, I am still willing to give Bill Gates the credit he deserves.

Bill Gates has made some famous Feynman lectures free for the public!

For those who don't know, Richard Feynman was a very famous physicist who worked on the Manhattan Project, won the Nobel Prize in physics for QED, and seemed to be involved in several other famous scientific activities. Many regard him as one of the top scientific minds ever.

In 1964, at Cornell, Feynman gave a famous series of lectures on physics highlighting the character of physical law. These lectures are very fascinating and have a lot of unique insights into a variety of subjects. Feynman had the ability to understand physical principles several different ways and could explain them in fairly simple terms. The lectures are truly masterpieces.

The lectures are available for free at Microsoft's Research Website. (Here is my only critique of the whole thing: Gates runs this great charity, but finds a way to make it so that his contributions require the use of Microsoft products. Go figure.)

Better At Math Than She Thinks

My wife, Rachel, has decided to apply for a Master's degree program in Public Administration and as a part of the application process she has to take the GRE. Aside from the Rachel's general dislike of standardized tests, she was very worried about the math portion of the test. Rachel hasn't taken a math class since Math 104 - "Quantitative Math" in her first semester of college and generally has a negative view of her mathematical abilities. So when she started studying for the GRE, she was far more concerned about the math section than the verbal or writing sections.

However, when she took her first practice test without any substantial math review, something interesting showed up in the results. She scored higher in the math section than the verbal section by a large margin - nearly 10 percentiles. Sure enough after some review of basic concepts that she had forgotten in the past 4-5 years, her math score went up by 10 more percentiles, making her math score nearly 15 percentiles higher than her verbal score (which also went up on her second try but only by 5 percentiles). Since the GRE is designed to test ability more than knowledge, the message is pretty clear: Rachel is innately better at math than she is in verbal skills even though she has believed (and been told by teachers) the opposite for at least the last 8 years.

To get a bit more background, Rachel was initially identified in elementary school as very good at math. She excelled in grade school math and that carried through to middle school. In high school, however, she had a teacher for freshman algebra who was male, poorly prepared to teach high school math (his bachelor's was in biology ed. and his masters in secondary ed.), and the baseball coach. She, along with many students in the class - especially female students - began to feel they didn't understand the material. With a poor foundation in basic algebra, when Rachel took intermediate algebra as a junior she was unprepared and begin to fall behind. After one difficult semester, Rachel's guidance counselor advised her to switch to a lower-level math class.

Rachel did so and once she was off the advanced math track, her high school math experience went downhill even faster. She took a class titled "AP Statistics" her senior year from a teacher that would often get confused and simply give-up trying to teach certain concepts. That teacher had taken 1 semester of statistics in college and hated it. No one from that "AP Statistics" class actually took the AP Statistics test.

In college, Rachel took "Quantitative Math" as she tried out various options for her major. Quantitative Math is a class designed to be the last math class you ever take. Instead of learning algebra, geometry, or trigonometry as a basis for learning more advanced concepts, this class focused on "practical" math like figuring out percentage discounts in supermarkets and computing interest from bank accounts. After taking it, Rachel was at a dead end in terms of a natural progression in math. She selected a major, Recreation Management, that didn't require any math at all, so she didn't take any more. It really is funny that only applying to graduate school finally proves that the grade school diagnosis of Rachel's potential in math was correct.

So what's the point of this rather long story? We have probably all had our share of really bad high school math teachers and we got through it. And the fact that there is a lot of untapped math ability out there is certainly nothing new.

If nothing else, this experience has shown me two things about math and by extension science education:

1. While students can overcome poor teachers, it is harder for women who face a lot of unintentional and even some intentional sexism when it comes to math and science.
2. As an aspiring professor, I need to make a special effort to reach out to those who have a lot of potential in math and science but may not think they do because of poor high school experiences. If we want more physicists, we need to go after those that have the ability but have been told they don't. They will likely be 1 or 2 out of a 100 students in large intro level classes, but they will be be there.