So, using standard trigonometry, and the fact that tan(θ) = opposite/ adjacent in flat space, you first calculate the size fluctuations should have grown in the universe when the CMB was emitted ~380,000 years after the big bang. (The opposite). Then you calculate the distance to those fluctuations from us. (The adjacent). And then, assuming all angles add up to 180 degrees and therefore tan(θ) = opposite/ adjacent applies, you solve for the angle θ that those fluctuations should make and then look at the CMB and ensure that the fluctuations are that size.
Then you make your measurement even more precise by turning again to our friend the power spectrum. The first peak in the power spectrum should be at the scale of the largest fluctuations in the CMB. The important formula is the peak at multiple l means the largest fluctuations are on the order of 180/l degrees.
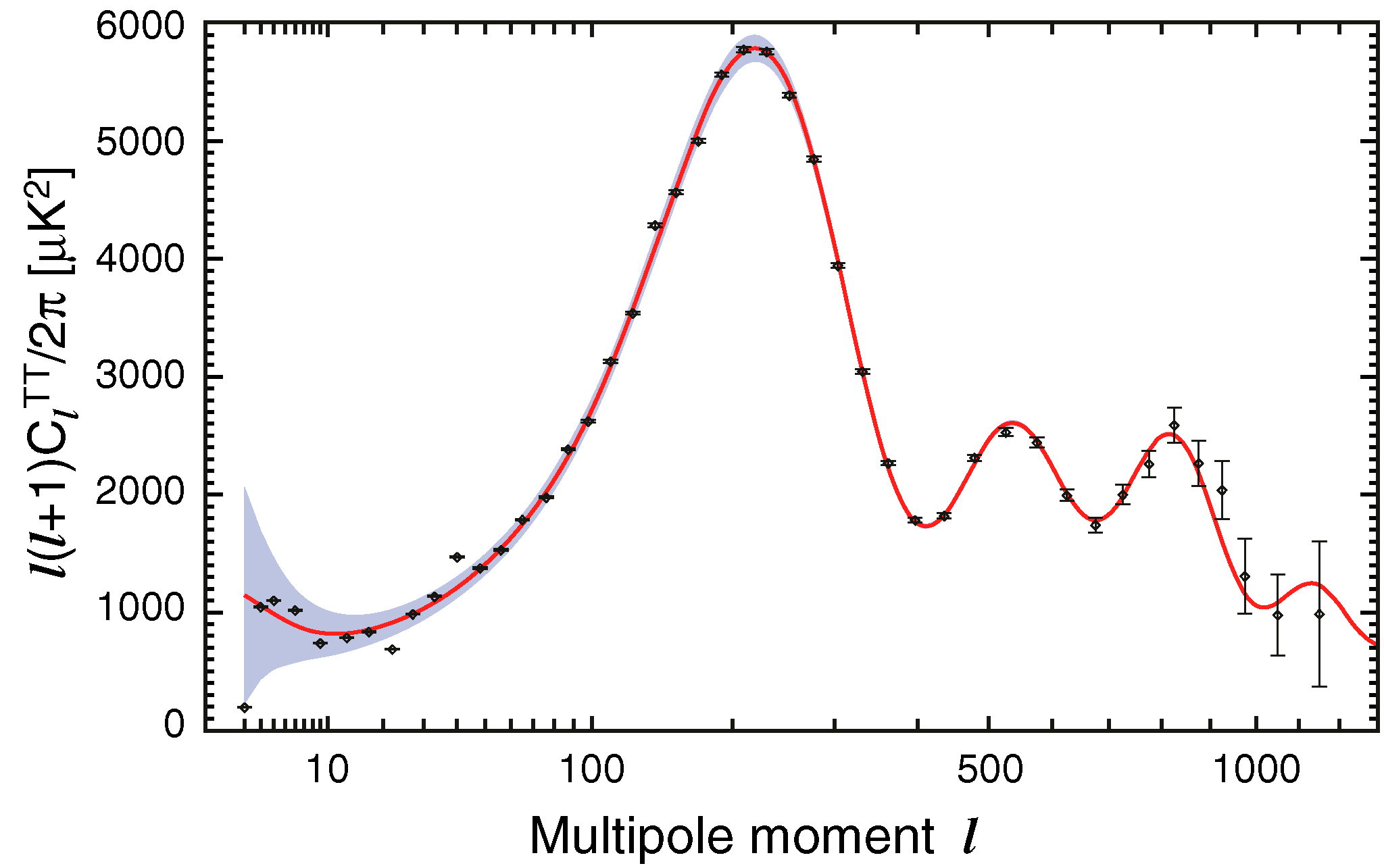The calculation: Anyways, using Ned Wright's Calculator I get the biggest fluctuation at the time of the CMB is about 0.64x10^6 light years across (opposite) and was emitted 41.5x10^6 light years away from us (adjacent) giving θ = 0.88 degrees which corresponds to a flat universe prediction is that the first peak should be at l ~ 205. (If you do this 100% correct and not just back of the envelop you should get l ~ 220)Anyways, as you can see from the power spectrum this is exactly where we see the first peak showing triangles in the space-time of our universe add up to 180 degrees and thus demonstrating our universe is flat!
So if the universe is flat, and we exist in the universe, then the earth is flat, also?
ReplyDeleteWow, and to think that the Flat Earthers were right all along! :P
rameumptom,
ReplyDeleteWell, if Flat Earthers use the fact the universe is flat to try to make their case I won't be surprised. :)
So how does the fact that the cc indicates a slightly accelerating current expansion fit into your flat thesis?
ReplyDeleteEric,
ReplyDeleteGood question. As things stand right now, the universe is still flat despite (actually aided by) the existence of the cosmological constant. This above calculation is true even thought the cc exists.
As for the future: another good question. Given we don't know what the cosmological constant is exactly I guess (though I am not an expert in exotic models) that with some scenarios the geometry changes.
However, if dark energy is a true cosmological constant that ends up dominating the universe the universe will go back to an exponential expansion (sort of like it was during inflation) and thus become even more "more flat".
Think living on the surface of a balloon. No matter what you local surface looks like, if the balloon inflates exponentially fast the area around you flattens out quickly.
Really interesting. When a statistician looks at a null hypothesis (say, X=0), he or she goes in thinking, "The null is almost certainly false," but the null might not be very strongly false (e.g. X might really be 0.00002 or something) and so the evidence might not let us say that it is false. Do you think of flat geometry that way -- flat means zero curvature and the universe is a priori almost certainly not flat -- or would you say that the universe had a flat geometry if it had a very small curvature?
ReplyDeleteAlso, could you give me a sense of what hangs on the geometry of the universe? It looks like a fascinating question in its own right -- just to satisfy curiosity (almost philosophical in character ;)) -- but does it have any practical implication if the universe is flat or not? Also, is the approach here just an update on Gauss' attempts to measure the curvature of space or is there something really new going on?
Jonathan,
ReplyDeleteA few things:
1. It was always assumed the universe had to be close to flat because if it had significant positive curvature it would recollapse to quickly for life to form and if it was too negative it would fly apart to quickly for galaxies to collapse by similar reasoning discussed here.
2. But this is a problem in another way known as the flatness problem: A flat universe is unstable in Einstein's equations!!! It is if you walked by a steep hill with a pinpoint top and found a ball is sitting perfectly on top. You would think it is very unnatural for a ball to be there unless there existed some mechanism that put it there.
3. This was one of the main motivations for inflation. Inflation would flatten out any universe like my balloon analogy discussed above providing a natural explanation for "why the ball is on the top of the hill".
3a. I actually misspoke to Eric above. Globally the universe will become open with positive dark energy but any local patch becomes flat. (Just like globally the balloon is not flat but local patches are). So, if inflation happened it would explain why our local observable patch is flat but technically we don't know what the global geometry is.
4. Therefore, what hangs on the geometry is: if flat we have to explain how given what is unstable in GR this could possibly be the case. Second, (and this is more practical) when computing distances to other objects in the universe, the geometry is important. For example, the geodesic or shortest path (which light would travel for instance) between me and Germany changes whether the earth is flat or curved.
Speaking of this "flat needed for life but flat is the unstable solution" issue, I'm surprised I have never heard the flatness of the universe used by those who want to show the universe seems fine tuned for life. :)
Is the video a little misleading about WMAP, or am I just misunderstanding when it says (starting about 2 minutes in), "In order to uncover the geometry of the universe, we need to be able to see all of it at one time. Fortunately, we have such pictures. This is an image of the entire universe in the microwave region of the spectrum"?
ReplyDeleteThe video seems to be suggesting that WMAP gives us a global picture of the geometry of spacetime, not just a local one. What am I missing?
Jonathan,
ReplyDeleteYes that is misleading and it should have said "In order to uncover the geometry of the *observable* universe, we need to be able to see all of it at one time."
There may be a lot more to the universe then what is observable and all we have really proven is that between us and where the photons of the CMB were emitted is flat.
In fact, if inflation is true then the observable universe is probably only a small speck of what actually exists. And furthermore, many modern theories suggest the patch that inflated was only a small patch of something larger and this leads to the idea of bubble universe forming etc..
This is all very speculative but is why we can only say we *know* that the observable universe is flat.
So cool! Man I wish I understood this stuff better. I'm jealous.
ReplyDeleteIf the universe resembles a rapidly spinning object that is bulging at its equator due to centrifugal force, how do we explain this unless the singularity that became our universe was also spinning rapidly before the Big Expansion? Spinning would theoretically cause a very dense, but very compact singularity to bulge at its equator and that bulge should maintain a good degree of integrity during an expansion. For all we know, the universe may be spinning rapidly within a larger reality and we may never be able to detect that spin.
ReplyDelete